tag:
последовательности
22.
\[\begin{array}{l}
{\text{Продолжи ряд:}}\\
{\text{а) 101}}{\text{, 1002}}{\text{, 10003}}{\text{, }}...\\
{\text{б) 4}}{\text{, 9}}{\text{, 6}}{\text{, 18}}{\text{, 8}}{\text{, 27}}{\text{, }}....
\end{array}\]
731.
Установи правило заполнения таблиц и определи какие числа должны стоять на месте знаков вопроса.
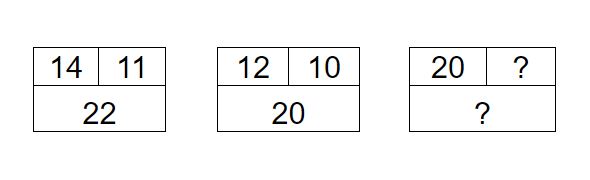

732.
Допиши следующие три числа:
1,2,3,2,4,6,3,6,9,...
1,2,3,2,4,6,3,6,9,...
809.
\[\begin{array}{l}
({\text{Теорема Цекендорфа}}) \hfill \\
{\text{Любое натуральное число либо само является числом Фибоначчи}}{\text{,}} \hfill \\
{\text{либо представляется единственным образом в виде суммы нескольких}} \hfill \\
{\text{чисел Фибоначчи (кроме }}{F_1}{\text{, его использовать нельзя)}}{\text{, среди которых}} \hfill \\
{\text{нет соседних}}{\text{. Например: }}444 = 377 + 55 + 8 + 3 + 1 = {F_{14}} + {F_{10}} + {F_6} + {F_4} + {F_2}. \hfill \\
{\text{а) Докажите}}{\text{, что каждое натуральное число возможно представить}} \hfill \\
{\text{таким образом}}{\text{.}} \hfill \\
{\text{б) Дана некоторая сумма чисел Фибоначчи}}{\text{, среди которых нет соседних}} \hfill \\
{\text{и самое большое число }}{F_n}.{\text{ Докажите}}{\text{, что эта сумма меньше }}{F_{n + 1}}. \hfill \\
{\text{в) Докажите}}{\text{, что представление каждого числа в виде указанной суммы}} \hfill \\
{\text{единственно}}{\text{.}} \hfill \\
\end{array} \]
2121.
\[\begin{array}{l}
{\text{Пусть }}f\left( x \right) = \frac{{x + 1}}{{x + 2}},{\text{ }}f\left( {f\left( x \right)} \right) = \frac{{{a_2}x + {b_2}}}{{{b_2}x + {c_2}}},{\text{ }}f\left( {f\left( {f\left( x \right)} \right)} \right) = \frac{{{a_3}x + {b_3}}}{{{b_3}x + {c_3}}}{\text{ и т}}{\text{.д}}{\text{.}} \hfill \\
{a_n},{b_n},{c_n} \in \mathbb{N}.{\text{ Докажите}}{\text{, что }}{a_n}{c_n} = b_n^2 + 1. \hfill \\
\end{array} \]
160.
\[\begin{array}{l}
{\text{Последовательность }}\left( {{b_n}} \right){\text{ задана условиями: }}{b_1} = 3,{\text{ }}{b_{n + 1}} = - \frac{1}{{{b_n}}}. \hfill \\
{\text{Найдите }}{b_3}. \hfill \\
\end{array} \]
163.
\[\begin{array}{l}
{\text{Последовательность }}\left( {{a_n}} \right){\text{ задана формулой }}{a_n} = \frac{{70}}{{n + 1}}.{\text{ Сколько членов}} \hfill \\
{\text{этой последовательности больше 6?}} \hfill \\
\end{array} \]
