\[\begin{array}{l} N = \frac{{\sqrt 2 {\pi ^{\frac{3}{2}}}}}{{4\Gamma {{\left( {\frac{3}{4}} \right)}^2}}} = \frac{{\pi \cdot G}}{2} = \frac{1}{4}{\rm B}\left( {\frac{1}{4},\frac{1}{2}} \right). \hfill \\ \Gamma {\text{ - гамма - функция;}} \hfill \\ G{\text{ - постоянная Гаусса;}} \hfill \\ {\rm B}{\text{ - бета - функция}}{\text{.}} \hfill \\ {\text{Докажите}}{\text{, что }}1 + \frac{{1 + \frac{{1 + \frac{{1 + \frac{{1 + ...}}{{2 + 3/7}}}}{{2 + 3/5}}}}{{2 + 3/3}}}}{{2 + 3/1}} = N. \hfill \\ {a_k} = 2 + \frac{3}{{2k - 1}}. \hfill \\ \end{array}\]

\[\begin{array}{l} {\text{Окружность }}\omega {\text{ и гипербола }}\Gamma {\text{ имеют общий центр}}{\text{. Докажите}}{\text{, что}} \hfill \\ {\text{инверсия }}\Gamma {\text{ относительно }}\omega {\text{ - лемниската Бернулли}}{\text{.}} \hfill \\ \end{array}\]

\[{\text{Докажите}}{\text{, что длина лемнискаты Бернулли }}\rho = \sqrt {\cos 2\varphi } {\text{ равна }}{\rm B}\left( {\frac{1}{4},\frac{1}{2}} \right).\]

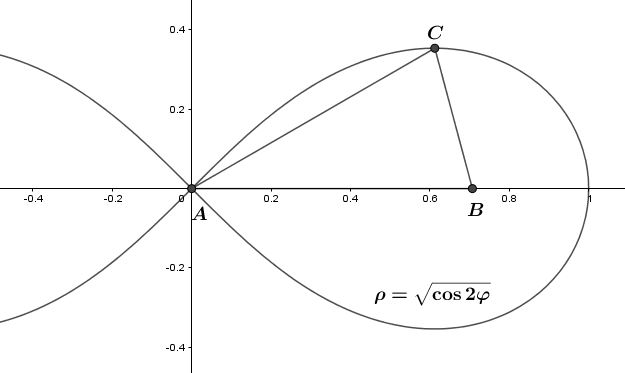
\[\begin{array}{l} {\text{Point }}B{\text{ is the focus of lemniscate }}\rho = \sqrt {\cos 2\varphi } ,{\text{ }}C{\text{ is the point of maximum}}{\text{, }}A\left( {0;0} \right). \hfill \\ {\text{Prove that }}\angle BAC = {30^ \circ }{\text{ and }}AB = AC. \hfill \\ \end{array} \]

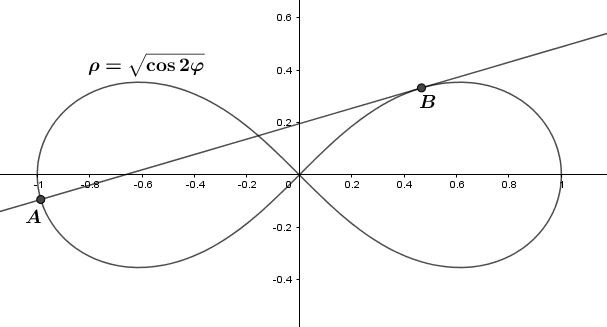
\[\begin{array}{l} {\text{Line }}AB{\text{ is normal line to lemniscate }}\rho {\text{ = }}\sqrt {\cos 2\varphi } {\text{ at point }}A{\text{ and is tangent to the lemniscate}} \hfill \\ {\text{at point }}B{\text{ (see pic}}{\text{.)}}{\text{. Find coordinates of points }}A{\text{ and }}B,{\text{ }}\left| {AB} \right|{\text{ and equation of line }}AB. \hfill \\ \end{array} \]