tag:
limits
Теорема
§
Теорема Штольца
616.
$$\eqalign{
\begin{array}{l}
{\text{Найти предел}}{\text{, пользуясь формулой Тейлора:}} \hfill \\
\mathop {\lim }\limits_{x \to \infty } \left( {{x^2} - {x^4}\ln \left( {1 + {x^{ - 2}}} \right)} \right). \hfill \\
\end{array}
} $$
620.
$$\eqalign{
\mathop {\lim }\limits_{x \to 0} \frac{{\ln \frac{{\sqrt {x + 1} + 1}}{2}}}{{{\mathop{\rm arctg}\nolimits} 4x}}
} $$
828.
\[\begin{array}{l}
{\text{Найдите число членов последовательности }}{x_n} = \frac{{2n - 1}}{{7n + 4}}{\text{, лежащих}} \hfill \\
{\text{вне интервала }}\left( {\frac{2}{7} - \frac{1}{{1000}};\frac{2}{7} + \frac{1}{{1000}}} \right). \hfill \\
\end{array}\]
829.
\[\begin{array}{l}
{\text{Для }}\varepsilon = 1,{\text{ }}\varepsilon = 0,1{\text{ и }}\varepsilon = 0,001{\text{ найдите соответствующие номера }}n{\text{,}} \hfill \\
{\text{начиная с которых будет выполняться неравенство }}\frac{3}{{\sqrt n }} < \varepsilon . \hfill \\
\end{array}\]
830.
\[\begin{array}{l}
{\text{Для каждого данного }}\varepsilon {\text{ найдите соответствующие номера }}N{\text{, что}} \hfill \\
{\text{при всех }}n \geqslant N{\text{ верно неравенство }}\left| {\frac{{3n - 1}}{{n + 2}} - 3} \right| < \varepsilon . \hfill \\
\varepsilon = {10^{ - 1}},{\text{ }}\varepsilon = {10^{ - 3}},{\text{ }}\varepsilon = {10^{ - 6}} \hfill \\
\end{array}\]
1701.
\[\mathop {\lim }\limits_{x \to \infty } \left( {\sqrt[5]{{\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right)\left( {x + 4} \right)\left( {x + 5} \right)}} - x} \right)\]
1735.
\[\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - {e^{ - x}}}}{{\sin x}}\]
1856.
\[\mathop {\lim }\limits_{x \to 0} \frac{{{a^x} + {b^x} - 2}}{{{c^x} + {d^x} - 2}}\]
1863.
\[\mathop {\lim }\limits_{x \to - \frac{\pi }{2}} \left( {\frac{{1 + \sin 13x}}{{1 + \sin 17x}}} \right)\]
1865.
\[\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \left( {\operatorname{tg} 3x\operatorname{tg} 8x} \right)\]
1975.
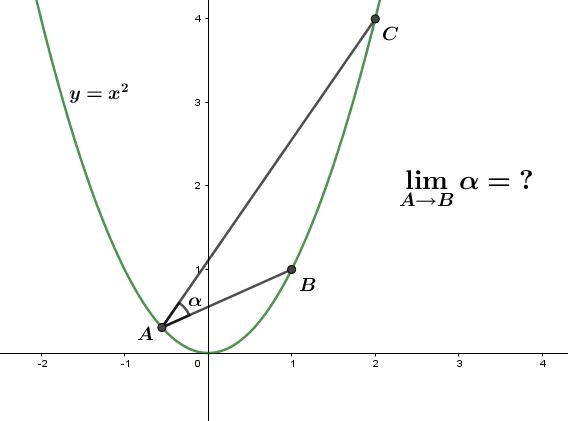
1981.
\[{\text{Докажите}}{\text{, что }}\mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{n}\sum\limits_{k = 1}^n {\left| {\sin k} \right|} } \right) = \frac{2}{\pi }.\]
1983.
\[{\text{Вычислите }}\mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{n}\sum\limits_{k = 1}^n {\sin \frac{k}{n}} } \right).\]
1984.
\[{\text{Докажите}}{\text{, что }}\mathop {\lim }\limits_{n \to + \infty } \left( {\prod\limits_{k = 1}^n {\cos \frac{k}{{{n^{\frac{3}{2}}}}}} } \right) = {e^{ - \frac{1}{6}}}.\]
2063.
\[\begin{array}{l}
{\text{Вычислите:}} \hfill \\
\mathop {\lim }\limits_{a \to 0 + } \left( {{a^{\frac{5}{3}}}\int\limits_a^{\frac{\pi }{2} - a} {\frac{{dx}}{{{{\left( {1 - \sin x} \right)}^{\frac{4}{3}}}}}} } \right) \hfill \\
\end{array}\]
2097.
\[{\text{Find }}\mathop {\lim }\limits_{n \to + \infty } \frac{n}{{\sqrt[n]{{n!}}}}.\]
2110.
\[\mathop {\lim }\limits_{x \to \frac{1}{2}} \frac{{{{\arcsin }^{\frac{1}{2}}}x - {{\left( {\frac{\pi }{6}} \right)}^{\frac{1}{2}}}}}{{{x^{\frac{1}{2}}} - {{\left( {\frac{1}{2}} \right)}^{\frac{1}{2}}}}}\]
2125.
$$\mathop {\lim }\limits_{n \to \infty } \frac{{{{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{3}}}} } \right)}^3} \cdot {{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{4}}}} } \right)}^4}}}{{{{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{2}}}} } \right)}^2} \cdot {{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{5}}}} } \right)}^5}}}$$
2152.
$$\begin{array}{l}
{a_1} = 0;{a_2} = 1; \hfill \\
{a_n} = \sqrt {\frac{{{a_{n - 1}} + {a_{n - 2}}}}{2} \cdot {a_{n - 1}}} ,{\text{ }}n \geqslant 3; \hfill \\
\mathop {\lim }\limits_{n \to \infty } {a_n} = \frac{1}{\pi }{\rm B}\left( {\frac{1}{2},\frac{3}{4}} \right) \hfill \\
\end{array} $$
