1618.
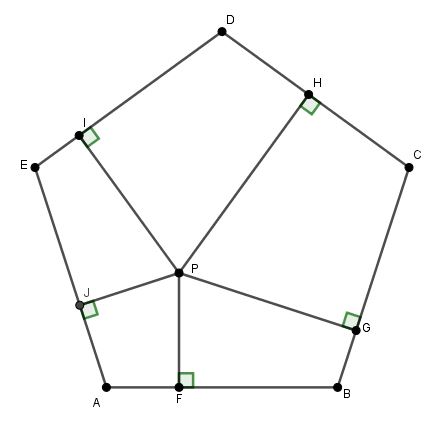
Внутри правильного пятиугольника ABCDE поставлена точка P, точки F,G,H,I,J - проекции точки P на стороны пятиугольника. Докажите, что сумма PF+PG+PH+PI+PJ не зависит от расположения точки P.

1785.
\[\begin{array}{l}
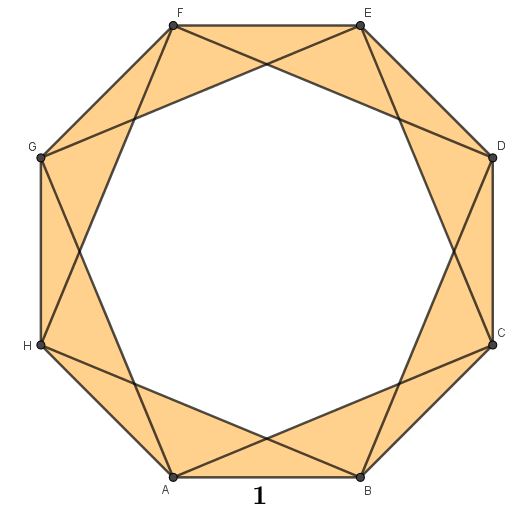
ABCDEFGH{\text{ - правильный восьмиугольник}}{\text{. }}AB = 1.{\text{ Найдите площадь}} \hfill \\
{\text{фигуры}}{\text{, отмеченной оранжевым цветом}}{\text{.}} \hfill \\
\end{array}\]

§
Формула площади четырёхугольника
\[\begin{array}{l}
{\text{Для произвольного четырёхугольника верна формула}} \hfill \\
S = \sqrt {\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)\left( {p - d} \right) - abcd{{\cos }^2}\theta } {\text{,}} \hfill \\
{\text{где }}S{\text{ - площадь четырёхугольника}}{\text{, }}p{\text{ - полупериметр}}{\text{, }}\theta {\text{ - полусумма}} \hfill \\
{\text{противоположных углов четырёхугольника}}{\text{.}} \hfill \\
\end{array}\]
1623.
\[\begin{array}{l}
{\text{В четырёхугольнике }}ABCD{\text{ }}AB = a,{\text{ }}BC = b,{\text{ }}CD = c,{\text{ }}AD = d.{\text{ Найдите}} \hfill \\
{\text{наибольшее возможное значение площади данного четырёхугольника}}{\text{.}} \hfill \\
\end{array}\]
1792.
\[\begin{array}{l}
{\text{Пусть }}p{\text{ и }}q{\text{ - диагонали ромба}}{\text{, }}r{\text{ - радиус вписанной окружности}}{\text{.}} \hfill \\
{\text{Докажите}}{\text{, что}} \hfill \\
r = \frac{{p \cdot q}}{{2\sqrt {{p^2} + {q^2}} }} \hfill \\
\end{array}\]
