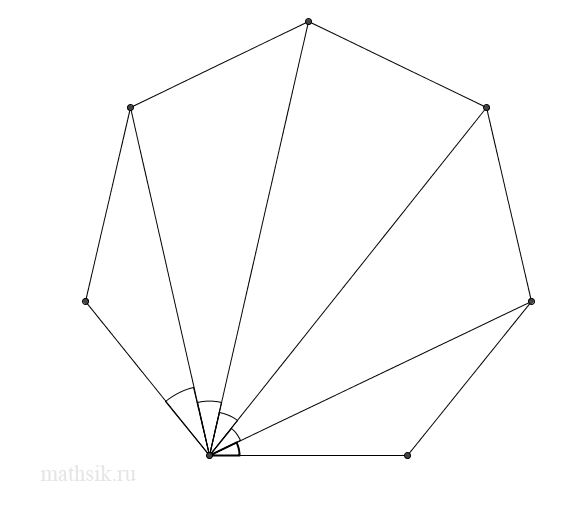
\[\begin{array}{l} {\text{В правильном многоугольнике проведены все диагонали из}}\\ {\text{одной из вершин}}{\text{. Докажите}}{\text{, что они разбивают внутренний}}\\ {\text{угол многоугольника на }}n - 2{\text{ равных угла}}{\text{.}} \end{array}\]

В правильный пятиугольник со стороной 1 вписан квадрат наибольшего размера. Найдите сторону квадрата.

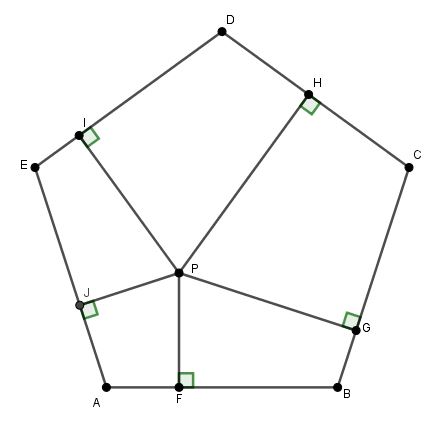
Внутри правильного пятиугольника ABCDE поставлена точка P, точки F,G,H,I,J - проекции точки P на стороны пятиугольника. Докажите, что сумма PF+PG+PH+PI+PJ не зависит от расположения точки P.

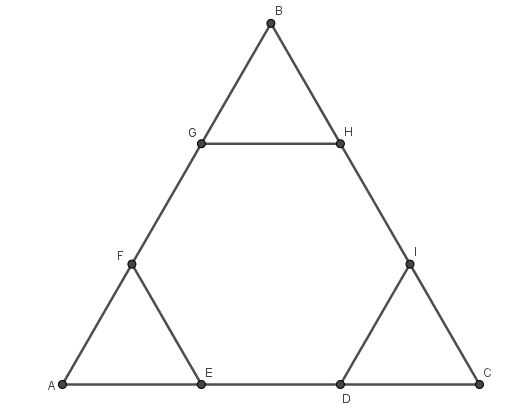
\[\begin{array}{l} {\text{Точки }}D,E,F,G,H,I{\text{ разбивают стороны правильного треугольника }}ABC \hfill \\ {\text{на три равные части}}{\text{. Площадь треугольника }}ABC{\text{ равна 9}}{\text{. Найдите площадь}} \hfill \\ {\text{шестиугольника }}DEFGHI. \hfill \\ \end{array}\]

Найдите площадь правильного восьмиугольника со стороной 1.

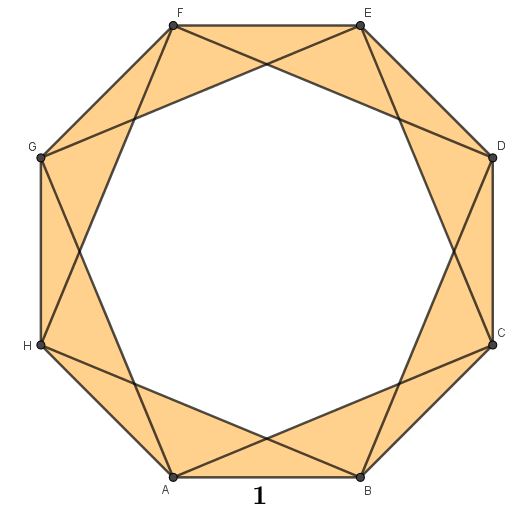
\[\begin{array}{l} ABCDEFGH{\text{ - правильный восьмиугольник}}{\text{. }}AB = 1.{\text{ Найдите площадь}} \hfill \\ {\text{фигуры}}{\text{, отмеченной оранжевым цветом}}{\text{.}} \hfill \\ \end{array}\]

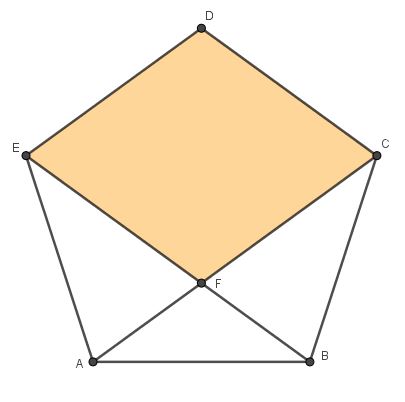
\[ABCDE{\text{ - правильный пятиугольник}}{\text{. Докажите}}{\text{, что }}EDCF{\text{ - ромб}}{\text{.}}\]

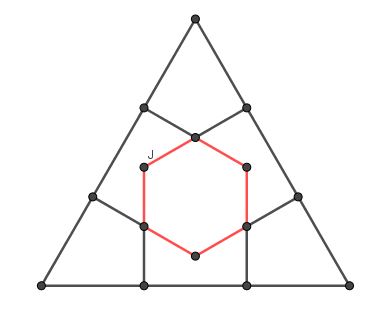
\[\begin{array}{l} {\text{Каждая сторона правильного треугольника делится двумя перпендикулярными}} \hfill \\ {\text{к стороне прямыми на три равные части}}{\text{, при этом образуется правильный}} \hfill \\ {\text{шестиугольник (см}}{\text{. рис}}{\text{.)}}{\text{. Найдите площадь этого шестиугольника}}{\text{, если сторона}} \hfill \\ {\text{треугольника равна 1}}{\text{.}} \hfill \\ \end{array}\]

\[\begin{array}{l} {\text{Правильный }}n{\text{ - угольник вписан в единичную окружность}}{\text{. Докажите}}{\text{, что}} \hfill \\ {\text{а) сумма квадратов длин всех сторон и всех диагоналей равна }}{n^2}; \hfill \\ {\text{б) сумма длин всех сторон и всех диагоналей равна }}n \cdot \operatorname{ctg} \frac{\pi }{{2n}}; \hfill \\ {\text{в) произведение длин всех сторон и всех диагоналей равно }}{n^{\frac{n}{2}}}. \hfill \\ \end{array}\]