2066.
\[\begin{array}{l}
{\text{Докажите}}{\text{, что}} \hfill \\
\prod\limits_{k = 1}^{n - 1} {\sin \frac{{\pi k}}{n}} = \frac{n}{{{2^{n - 1}}}}. \hfill \\
\end{array}\]
Igore
63 days ago
2154.
$$\eqalign{
& s > 0,{\text{ }}s \ne \frac{1}{n}; \cr
& \cfrac{1}{{\cfrac{s}{{1 + \cfrac{{s - 1}}{{1 + \cfrac{{2s}}{{1 + \cfrac{{2s - 1}}{{1 + \cfrac{{3s}}{{1 + \cfrac{{3s - 1}}{{1 + ...}}}}}}}}}}}}}} = {s^{\frac{1}{s} - 1}} \cdot {e^{\frac{1}{s}}} \cdot \Gamma \left( {\frac{1}{s},\frac{1}{s}} \right) \cr} $$
Igore
63 days ago
1978.
\[\coth x = \frac{{{e^{2x}} + 1}}{{{e^{2x}} - 1}} = \frac{1}{x} + \frac{{\frac{1}{{1 \cdot 3}}}}{{\frac{1}{x} + \frac{{\frac{1}{{3 \cdot 5}}}}{{\frac{1}{x} + \frac{{\frac{1}{{5 \cdot 7}}}}{{\frac{1}{x} + ...}}}}}}.\]
Igore
71 days ago
§
$$\eqalign{
& \cos \left( {p\arccos x} \right) = \cosh \left( {p\ln \left( {x + \sqrt {{x^2} - 1} } \right)} \right) = \cr
& \frac{1}{2}\left( {{{\left( {x + \sqrt {{x^2} - 1} } \right)}^p} + {{\left( {x + \sqrt {{x^2} - 1} } \right)}^{ - p}}} \right) \cr} $$Igore
121 days ago
§
$$\int\limits_0^{ + \infty } {{e^{ - st}}{t^{x - 1}}dt} = \frac{{\Gamma \left( x \right)}}{{{s^x}}}$$Igore
253 days ago
§
\[\left[ {{\text{Ламберт}}} \right]\]
$$\operatorname{tg} x = \cfrac{x}{{1 - \cfrac{{{x^2}}}{{3 - \cfrac{{{x^2}}}{{5 - \cfrac{{{x^2}}}{{7 - ...}}}}}}}} = \cfrac{1}{{\cfrac{1}{x} - \cfrac{1}{{\cfrac{3}{x} - \cfrac{1}{{\cfrac{5}{x} - \cfrac{1}{{\cfrac{7}{x} - \cfrac{1}{{...}}}}}}}}}}$$Igore
254 days ago
§
$$\operatorname{arctg} x = \cfrac{x}{{1 + \cfrac{{{x^2}}}{{3 + \cfrac{{4{x^2}}}{{5 + \cfrac{{9{x^2}}}{{7 + \cfrac{{16{x^2}}}{{...}}}}}}}}}}$$Igore
254 days ago
1722.
\[\tanh \frac{1}{n} = \frac{1}{{n + \frac{1}{{3n + \frac{1}{{5n + \frac{1}{{7n + \frac{1}{{...}}}}}}}}}}\]
Igore
254 days ago
§
$$\Gamma \left( x \right)\Gamma \left( {x + \frac{1}{2}} \right) = {2^{1 - 2x}}\sqrt \pi \Gamma \left( {2x} \right)$$Igore
254 days ago
§
Разложение Куммера
$$\ln \Gamma \left( x \right) = \ln \sqrt {2\pi } + \sum\limits_{n = 1}^{ + \infty } {\frac{1}{{2n}}\cos \left( {2\pi nx} \right)} + \sum\limits_{n = 1}^{ + \infty } {\frac{{\gamma + \ln \left( {2\pi n} \right)}}{{\pi n}}\sin \left( {2\pi nx} \right)} ,{\text{ }}0 < x < 1.$$
Igore
256 days ago
2156.
$$\eqalign{
& \cfrac{1}{{1 + x}} + \cfrac{{\cfrac{1}{{1 + x/2}} + \cfrac{{\cfrac{1}{{1 + x/3}} + \cfrac{{...}}{{3/x}}}}{{2/x}}}}{{1/x}} = \cr
& = x \cdot {\left( { - x} \right)^{ - x}} \cdot \left( {\Gamma \left( x \right) - \Gamma \left( {x, - x} \right)} \right) \cr
& = x \cdot {\left( { - x} \right)^{ - x}}\int\limits_0^{ - x} {{t^{x - 1}}{e^{ - t}}dt} = x{\left( { - x} \right)^{ - x}}\gamma \left( {x, - x} \right) \cr} $$
Igore
341 days ago
2155.
$$1 + \cfrac{{1 + \cfrac{{1 + \cfrac{{1 + \cfrac{{1 + ...}}{{4s + 1}}}}{{3s + 1}}}}{{2s + 1}}}}{{s + 1}} + \cfrac{1}{{\cfrac{s}{{1 + \cfrac{{s - 1}}{{1 + \cfrac{{2s}}{{1 + \cfrac{{2s - 1}}{{1 + \cfrac{{3s}}{{1 + \cfrac{{3s - 1}}{{1 + ...}}}}}}}}}}}}}} = {s^{\frac{1}{s} - 1}}{e^{\frac{1}{s}}}\Gamma \left( {\frac{1}{s}} \right)$$
\[s > 0,{\text{ }}s \ne \frac{1}{n};\]
Igore
350 days ago
2153.
$$1 + \cfrac{{\cfrac{1}{{1 \cdot s}}}}{{1 + \cfrac{{\cfrac{1}{{2 \cdot s}}}}{{1 + \cfrac{{\cfrac{1}{{3 \cdot s}}}}{{1 + ...}}}}}} = 1 + \cfrac{{1 + \cfrac{{1 + \cfrac{{1 + ...}}{{3s + 1}}}}{{2s + 1}}}}{{1s + 1}} = \sum\limits_{n = 0}^{ + \infty } {\frac{1}{{\prod\limits_{k = 1}^n {\left( {sk + 1} \right)} }}} = {s^{\frac{1}{s} - 1}}{e^{\frac{1}{s}}}\left( {\Gamma \left( {\frac{1}{s}} \right) - \Gamma \left( {\frac{1}{s},\frac{1}{s}} \right)} \right)$$
Igore
351 days ago
762.
Найдите на картинке все группы изоморфных графов.
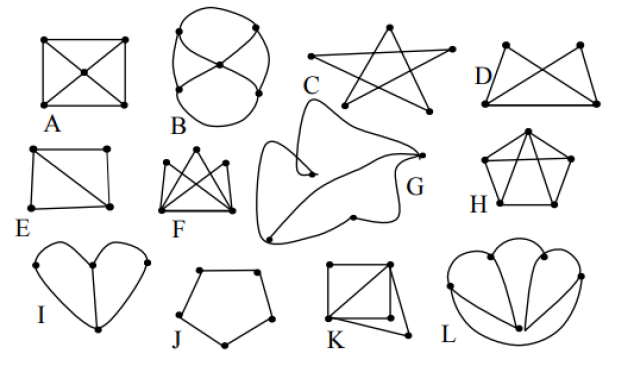

assa
402 days ago
2152.
$$\begin{array}{l}
{a_1} = 0;{a_2} = 1; \hfill \\
{a_n} = \sqrt {\frac{{{a_{n - 1}} + {a_{n - 2}}}}{2} \cdot {a_{n - 1}}} ,{\text{ }}n \geqslant 3; \hfill \\
\mathop {\lim }\limits_{n \to \infty } {a_n} = \frac{1}{\pi }{\rm B}\left( {\frac{1}{2},\frac{3}{4}} \right) \hfill \\
\end{array} $$
Igore
509 days ago
2151.
$$\prod\limits_{k = 1}^{ + \infty } {\frac{{{{\left( {3k + 2} \right)}^3}}}{{27k{{\left( {k + 1} \right)}^2}}}} = {\left( {\frac{3}{{2\Gamma \left( {\frac{2}{3}} \right)}}} \right)^3}$$
Igore
552 days ago
2150.
$$\prod\limits_{k = 1}^{ + \infty } {\frac{{2k\left( {2k + 2} \right)}}{{{{\left( {2k + 1} \right)}^2}}}} = \frac{\pi }{4}$$
Igore
552 days ago
2149.
$$\eqalign{
& \prod\limits_{k = 1}^{ + \infty } {{{\left( {1 + \frac{1}{{2k}}} \right)}^{{{\left( { - 1} \right)}^k}}}} = \frac{4}{{{\rm B}\left( {\frac{1}{2},\frac{1}{4}} \right)}} \cr
& \prod\limits_{k = 1}^{ + \infty } {{{\left( {1 - \frac{1}{{2k}}} \right)}^{{{\left( { - 1} \right)}^k}}}} = \frac{1}{\pi }{\rm B}\left( {\frac{1}{2},\frac{1}{4}} \right) \cr
& \prod\limits_{k = 1}^{ + \infty } {\left( {1 + \frac{{{{\left( { - 1} \right)}^{k + 1}}}}{{2k}}} \right)} = \frac{1}{{2\pi }}{\rm B}\left( {\frac{1}{4},\frac{1}{4}} \right) \cr} $$
Igore
552 days ago
2148.
$$\int\limits_0^{ + \infty } {\operatorname{arctg} \left( {{e^{ - x}}} \right)dx} $$
Igore
589 days ago
2147.
$$\sum\limits_{k = 0}^{ + \infty } {\frac{1}{{\cosh \left( {\pi k} \right)}}} = \frac{1}{2} + \frac{1}{{{\rm B}\left( {\frac{3}{4},\frac{3}{4}} \right)}}.$$
$$\sum\limits_{k = 0}^{ + \infty } {\frac{{{{\left( { - 1} \right)}^k}}}{{\cosh \left( {\pi k} \right)}}} = \frac{1}{2} + \frac{1}{{{\rm B}\left( {\frac{1}{2},\frac{3}{4}} \right)}}.$$
Igore
606 days ago
2146.
$$\int\limits_0^{ + \infty } {\frac{1}{{\sqrt {{e^x} - 1} }}dx} $$
Igore
607 days ago
2145.
$$1 + \cfrac{1}{{1 + \cfrac{2}{{1 + \cfrac{3}{{1 + \cfrac{4}{{1 + ...}}}}}}}} = \cfrac{2}{{1 + \cfrac{1}{{1 + \cfrac{4}{{1 + \cfrac{3}{{... + \cfrac{{2n}}{{1 + \cfrac{{2n - 1}}{{1 + ...}}}}}}}}}}}}$$
Igore
609 days ago
2144.
$$\int\limits_0^{\frac{{2\pi }}{3}} {{{\ln }^2}\left( {2\cos \frac{x}{2}} \right)dx} $$
Igore
611 days ago
2143.
$$\operatorname{tg} \left( {\frac{1}{4}\operatorname{arctg} \frac{4}{3}} \right) = \sqrt 5 - 2.$$
$$\operatorname{tg} \left( {\frac{1}{3}\operatorname{arctg} \frac{{\sqrt 5 }}{7}} \right) = \frac{{3\sqrt 3 - 2\sqrt 5 }}{7}$$
$$\operatorname{tg} \left( {\frac{1}{4}\operatorname{arctg} \frac{{\sqrt 5 }}{2}} \right) = \sqrt 6 - \sqrt 5 $$
$$\operatorname{tg} \left( {\frac{1}{4}\operatorname{arctg} \frac{1}{8}} \right) = \frac{{\sqrt 7 }}{7}$$
Igore
621 days ago
2142.
$$\sum\limits_{k = 0}^{ + \infty } {\dfrac{{{x^{k + 1}}}}{{k{!^s}}}} = x + \dfrac{{{x^2} + \dfrac{{{x^3} + \dfrac{{{x^4} + \dfrac{{{x^5} + ...}}{{{4^s}}}}}{{{3^s}}}}}{{{2^s}}}}}{{{1^s}}},{\text{ }}s > 0$$
Igore
624 days ago
2141.
\[{\text{Вычислите:}}\]
$$\sqrt[4]{{18 - \sqrt[4]{{18 - \sqrt[4]{{18 - ...}}}}}}$$
Igore
626 days ago
2140.
$$\sqrt[3]{{6 + \sqrt[3]{{6 + \sqrt[3]{{6 + \sqrt[3]{{6 + ...}}}}}}}}=x .$$
Igore
626 days ago
2139.
$$\prod\limits_{k = 1}^{ + \infty } {\frac{{2k\left( {4k + 3} \right)}}{{\left( {2k + 1} \right)\left( {4k + 1} \right)}}} = \frac{1}{6}{\rm B}\left( {\frac{1}{2},\frac{1}{4}} \right)$$
Igore
627 days ago
2138.
$$\frac{{{\pi ^2}}}{6} = \frac{3}{2} + \frac{1}{{7 - \frac{{{1^4}}}{{11 - \frac{{{2^4}}}{{19 - \frac{{...}}{{... - \frac{{{n^4}}}{{2{n^2} - 2n + 7 - ...}}}}}}}}}}$$
Igore
628 days ago
2137.
$$\sum\limits_{k = 0}^{ + \infty } {{{\left( { - 1} \right)}^k}{{\left( {\prod\limits_{i = 1}^k {\frac{{2i - 1}}{{2i}}} } \right)}^2}} = \frac{1}{{2\pi }}{\rm B}\left( {\frac{1}{2},\frac{1}{4}} \right) = \frac{{\sqrt {2\pi } }}{{2\Gamma {{\left( {\frac{3}{4}} \right)}^2}}}.$$
Igore
631 days ago
2136.
$$\begin{array}{l}
\frac{1}{2} + \frac{2}{{1 + 2 \cdot \left( {\frac{1}{4} + \frac{4}{{1 + 4 \cdot \left( {\frac{1}{6} + \frac{6}{{1 + 6 \cdot \left( {...} \right)}}} \right)}}} \right)}} = \frac{{{\pi ^2}}}{8} - 1 + G, \hfill \\
{\text{где }}G{\text{ - постоянная Каталана}}{\text{.}} \hfill \\
\end{array} $$
Igore
634 days ago
2135.
$$\sum\limits_{k = 0}^{ + \infty } {\frac{{{{\left( { - 1} \right)}^k}}}{{{{\left( {2k + 1} \right)}^3}}}} = \frac{{{\pi ^3}}}{{32}}$$
Igore
634 days ago
2134.
$$\sum\limits_{k = 1}^{ + \infty } {\frac{1}{{{\pi ^2}{k^2} + 1}}} $$
Igore
642 days ago
2133.
$$\int\limits_0^{ + \infty } {\frac{{\sin x}}{{{e^{\pi x}} - 1}}dx} = \frac{1}{{{e^2} - 1}}$$
Igore
643 days ago
2132.
$$\int\limits_0^{ + \infty } {\frac{{{x^{2n}}}}{{{e^{\pi x}} - 1}}dx} = \frac{{\left( {2n} \right)!\zeta \left( {2n + 1} \right)}}{{{\pi ^{2n + 1}}}},{\text{ }}n \in \mathbb{N}.$$
Igore
643 days ago
2131.
$$\int\limits_0^{ + \infty } {\frac{x}{{{x^{\ln x}}}}dx} $$
Igore
662 days ago
2130.
\[\begin{array}{l}
{\text{Найдите криволинейный интеграл 1 рода }}\int\limits_l {\sqrt {1 - {x^2} - {y^2}} dl} \hfill \\
{\text{по дуге лемнискаты }}{\left( {{x^2} + {y^2}} \right)^2} = {x^2} - {y^2},{\text{ }}x \geqslant 0,{\text{ }}y \geqslant 0. \hfill \\
\end{array} \]
Igore
674 days ago
2129.
$$\int\limits_0^{ + \infty } {\frac{{\sin \left( {{x^2}} \right)}}{{{e^{{x^2}}}}}dx} = \frac{1}{4}\sqrt {\frac{\pi }{{1 + \sqrt 2 }}} $$
$$\int\limits_0^{ + \infty } {\frac{{\cos \left( {{x^2}} \right)}}{{{e^{{x^2}}}}}dx} = \frac{1}{4}\sqrt {\pi \cdot \left( {1 + \sqrt 2 } \right)} $$
$$\int\limits_0^{ + \infty } {\frac{{\cos \left( {{x^2}} \right)}}{{{e^{{x^2}}}}}dx} = \frac{1}{4}\sqrt {\pi \cdot \left( {1 + \sqrt 2 } \right)} $$
Igore
676 days ago
2128.
$$\begin{array}{l}\cos \frac{\pi }{{17}} \cdot \cos \frac{{4\pi }}{{17}} = \frac{{1 + \sqrt {17} + \sqrt {34 + 2\sqrt {17} } }}{{16}}
\hfill \\
\frac{1}{{\cos \frac{\pi }{{17}}}} + \frac{1}{{\cos \frac{{2\pi }}{{17}}}} - \frac{1}{{\cos \frac{{4\pi }}{{17}}}} + \frac{1}{{\cos \frac{{8\pi }}{{17}}}} = 2\sqrt {17 + 4\sqrt {17} }\end{array} $$
Igore
706 days ago
2011.
\[\int\limits_0^1 {\frac{{\arctan \left( {{x^k}} \right)}}{x}dx} \]
Igore
714 days ago
2127.
\[{\text{Найдите }}y \in \mathbb{N}.\]
$$\frac{1}{{\sqrt[3]{{{{\cos }^2}\frac{{2\pi }}{9}}}}} + \frac{1}{{\sqrt[3]{{{{\cos }^2}\frac{{4\pi }}{9}}}}} + \frac{1}{{\sqrt[3]{{{{\cos }^2}\frac{{8\pi }}{9}}}}} = \sqrt[3]{{\frac{{y\left( {\sqrt[3]{9} - 1} \right)}}{{\sqrt[3]{9} - 2}}}}$$
Igore
724 days ago
2126.
\[{\text{Найдите }}x \in \mathbb{N}.\]
$$\frac{1}{{\sqrt[3]{{\cos \frac{{2\pi }}{9}}}}} + \frac{1}{{\sqrt[3]{{\cos \frac{{4\pi }}{9}}}}} + \frac{1}{{\sqrt[3]{{\cos \frac{{8\pi }}{9}}}}} = \sqrt[3]{{x\left( {\sqrt[3]{9} - 1} \right)}}$$
Igore
724 days ago
2125.
$$\mathop {\lim }\limits_{n \to \infty } \frac{{{{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{3}}}} } \right)}^3} \cdot {{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{4}}}} } \right)}^4}}}{{{{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{2}}}} } \right)}^2} \cdot {{\left( {\sum\limits_{k = 1}^n {{k^{\frac{1}{5}}}} } \right)}^5}}}$$
Igore
729 days ago
2124.
$$\begin{array}{l}
{\text{Найдите целое число }}x,{\text{ которое удовлетворяет равенству}}{\text{.}} \hfill \\
\sqrt[4]{{3\sqrt 5 - 1 - \sqrt {6\left( {5 - \sqrt 5 } \right)} }} + \sqrt[4]{{3\sqrt 5 - 1 + \sqrt {6\left( {5 - \sqrt 5 } \right)} }} = \sqrt {x + \sqrt {6 + 6\sqrt 5 } } . \hfill \\
\end{array} $$
Igore
729 days ago
2123.
$$\int\limits_0^{ + \infty } {\frac{1}{{\cosh \sqrt x }}dx} $$
Igore
739 days ago
2122.
$%\begin{array}{l}
{\text{Выпуклый пятиугольник }}ABCDE{\text{ вписан в окружность}}{\text{. }}AB = 1,{\text{ }}BC = 2,{\text{ }}CD = 3,{\text{ }}DE = 4,{\text{ }}AE = \frac{{6\sqrt {14} - 2}}{5}. \hfill \\
{\text{Найдите радиус описанной окружности}}{\text{.}} \hfill \\
\end{array} $%
Igore
875 days ago
2121.
\[\begin{array}{l}
{\text{Пусть }}f\left( x \right) = \frac{{x + 1}}{{x + 2}},{\text{ }}f\left( {f\left( x \right)} \right) = \frac{{{a_2}x + {b_2}}}{{{b_2}x + {c_2}}},{\text{ }}f\left( {f\left( {f\left( x \right)} \right)} \right) = \frac{{{a_3}x + {b_3}}}{{{b_3}x + {c_3}}}{\text{ и т}}{\text{.д}}{\text{.}} \hfill \\
{a_n},{b_n},{c_n} \in \mathbb{N}.{\text{ Докажите}}{\text{, что }}{a_n}{c_n} = b_n^2 + 1. \hfill \\
\end{array} \]
Igore
889 days ago
2120.
\[{\text{Prove that}}\]
$$\sum\limits_{k = 0}^n {\frac{{\left( {2k} \right)!!}}{{\left( {2k + 1} \right)!!}}} = \frac{{2n + 3}}{2} \cdot {\rm B}\left( {\frac{1}{2},n + 2} \right) - 1.$$
Igore
913 days ago
2119.
$$\int\limits_0^{ + \infty } {\frac{{dx}}{{{{\cosh }^{2n}}x}}} ,{\text{ }}\int\limits_0^{ + \infty } {\frac{{dx}}{{{{\cosh }^{2n + 1}}x}}} $$
Igore
913 days ago
2118.
$$\int\limits_0^{ + \infty } {\frac{{dx}}{{\sqrt {\cosh x} }}} $$
Igore
913 days ago
2107.
$$\int\limits_0^{ + \infty } {\frac{{{x^{2n}}}}{{\cosh x}}dx} = \left| {{E_{2n}}} \right| \cdot {\left( {\frac{\pi }{2}} \right)^{2n + 1}},$$
\[n \in \mathbb{N}.\]
Igore
913 days ago
2117.
$$\int\limits_0^{ + \infty } {\frac{{\left| {\sin x} \right|}}{{{e^x}}}dx} $$
Igore
914 days ago
2116.
$$\mathop {\lim }\limits_{n \to \infty } \left( {n \cdot \prod\limits_{k = 1}^n {\frac{{1 + {{\left( {2k} \right)}^2}}}{{1 + {{\left( {2k + 1} \right)}^2}}}} } \right) = \tanh \frac{\pi }{2}$$
Igore
916 days ago
2115.
\[\int\limits_0^{ + \infty } {\frac{x}{{{e^x} + {e^{ - x}}}}dx} \]
Igore
926 days ago
2113.
\[{\text{Simplify }}\sqrt[n]{{a\sqrt[n]{{a\sqrt[n]{{a\sqrt[n]{{...}}}}}}}},{\text{ }}a > 0.\]
Igore
932 days ago
2112.
\[{\text{Evaluate }}f\left( x \right) = {x^{{x^{{x^{...}}}}}}{\text{ (infinite power tower) at }}x = {e^{\frac{1}{e}}}.{\text{ Prove that }}f\left( x \right) = + \infty {\text{ if }}x > {e^{\frac{1}{e}}}.\]
Igore
935 days ago
2111.
\[{\text{Evaluate }}{\left( {\frac{1}{4}} \right)^{{{\left( {\frac{1}{4}} \right)}^{{{\left( {\frac{1}{4}} \right)}^{...}}}}}}{\text{ (infinite power tower)}}{\text{.}}\]
Igore
935 days ago
2110.
\[\mathop {\lim }\limits_{x \to \frac{1}{2}} \frac{{{{\arcsin }^{\frac{1}{2}}}x - {{\left( {\frac{\pi }{6}} \right)}^{\frac{1}{2}}}}}{{{x^{\frac{1}{2}}} - {{\left( {\frac{1}{2}} \right)}^{\frac{1}{2}}}}}\]
Igore
936 days ago
2109.
$%\begin{array}{l}
{\text{Пусть }}0 < a < 1.{\text{ Найдите уравнение}}{\text{, корнем которого является число }}x = {a^{{a^{{a^{a...}}}}}} \hfill \\
{\text{(бесконечная башня степеней)}}{\text{. (В записи уравнения не должно содержаться }}{a^{{a^{{a^{a...}}}}}}{\text{)}}{\text{.}} \hfill \\
\end{array} $%
Igore
937 days ago
§
$$\sin x = 2\sin \frac{x}{2}\cos \frac{x}{2} = 4\sin \frac{x}{4}\cos \frac{x}{4}\cos \frac{x}{2} = ... = {2^n}\sin \frac{x}{{{2^n}}}\prod\limits_{k = 1}^n {\cos \frac{x}{{{2^n}}}} $$
Igore
938 days ago
