512.
$$\eqalign{
{\text{На сторонах }}AC{\text{ и }}BC{\text{ треугольника }}ABC{\text{ вне треугольника построены}} \hfill \\
{\text{квадраты }}ACDE{\text{ и }}BFKC.{\text{ Точка }}M{\text{ - середина стороны }}AB. \hfill \\
{\text{а) Докажите}}{\text{, что }}CM = \frac{1}{2}DK. \hfill \\
{\text{б) Найдите расстояние от точки }}M{\text{ до центров квадратов}}{\text{, если }}AC = 10, \hfill \\
BC = 32{\text{ и }}\angle ACB = {30^ \circ }. \hfill \\
} $$
513.
На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что \[\cos \angle ABC = \frac{1}{6}\]. В каком отношении прямая DL делит сторону AB?
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что \[\cos \angle ABC = \frac{1}{6}\]. В каком отношении прямая DL делит сторону AB?
563.
Окружность проходит через вершины B и C треугольника ABC и пересекает AB и AC в точках \[{C_1}\] и \[{B_1}\] соответственно.
а) Докажите, что треугольник ABC подобен треугольнику \[A{B_1}{C_1}\].
б) Вычислите длину стороны BC и радиус данной окружности, если \[\angle A = {135^ \circ }\], \[{B_1}{C_1} = 10\] и площадь треугольника \[A{B_1}{C_1}\] в семь раз меньше площади четырёхугольника \[BC{B_1}{C_1}\].
а) Докажите, что треугольник ABC подобен треугольнику \[A{B_1}{C_1}\].
б) Вычислите длину стороны BC и радиус данной окружности, если \[\angle A = {135^ \circ }\], \[{B_1}{C_1} = 10\] и площадь треугольника \[A{B_1}{C_1}\] в семь раз меньше площади четырёхугольника \[BC{B_1}{C_1}\].
380.
\[\begin{array}{l}{\text{В треугольнике }}ABC{\text{ известно}}{\text{, что }}\angle BAC = {60^ \circ },{\text{ }}\angle ABC = {45^ \circ }.{\text{ Продолжения}}\\{\text{высот треугольника }}ABC{\text{ пересекают описанную около него окружность в}}\\{\text{точках }}M,N,P.\\{\text{а) Докажите}}{\text{, что треугольник }}MNP{\text{ прямоугольный}}{\text{.}}\\{\text{б) Найдите площадь треугольника }}MNP{\text{, если известно}}{\text{, что }}BC = 10.\end{array}\]
542.
В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC=8.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC=8.
1109.
На прямой, содержащей биссектрису AD прямоугольного треугольника ABC с прямым углом C, взята точка E, удалённая от вершины A на расстояние, равное \[\sqrt {26} \]. Найдите площадь треугольника BCE, если BC = 5, AC = 12.
893.
\[\begin{array}{l}
{\text{Окружности радиусов 1 и 7 с центрами }}{O_1}{\text{ и }}{O_2}{\text{ соответственно касаются}} \hfill \\
{\text{в точке }}A.{\text{ Прямая}}{\text{, проходящая через точку }}A{\text{, вторично пересекает меньшую}} \hfill \\
{\text{окружность в точке }}B{\text{, а большую - в точке }}C.{\text{ Найдите площадь треугольника}} \hfill \\
BC{O_2}{\text{, если }}\angle AB{O_1} = {22,5^ \circ }. \hfill \\
\end{array}\]
1124.
Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что \[\angle ABM = {30^ \circ }\].
б) Найдите расстояние от центра прямоугольника до прямой CM, если \[BC = 6\sqrt {21} \].
а) Докажите, что \[\angle ABM = {30^ \circ }\].
б) Найдите расстояние от центра прямоугольника до прямой CM, если \[BC = 6\sqrt {21} \].
1122.
Через вершину T остроугольного треугольника TCD проведена касательная l к окружности, описанной около этого треугольника. Точки A и B - основания перпендикуляров, опущенных из точек D и C соответственно на прямую l, TH - высота треугольника TCD.
а) Докажите, что угол HTC равен углу TDA.
б) Найдите TH, если BC=\[2\sqrt 2 \], AD=\[4\sqrt 2 \].
а) Докажите, что угол HTC равен углу TDA.
б) Найдите TH, если BC=\[2\sqrt 2 \], AD=\[4\sqrt 2 \].
1278.
Вершины K и L квадрата KLMN с центром O лежат на стороне AB треугольника ABC, а вершины M и N - на сторонах BC и AC соответственно. Высота CH треугольника ABC проходит через точку O и пересекает отрезок MN в точке D, причём CD = DO = OH.
а) Докажите, что треугольник ABC равнобедренный и прямоугольный.
б) Пусть прямая AD пересекает сторону CD в точке Q. Найдите AQ, если сторона квадрата KL = 5.
а) Докажите, что треугольник ABC равнобедренный и прямоугольный.
б) Пусть прямая AD пересекает сторону CD в точке Q. Найдите AQ, если сторона квадрата KL = 5.
1185.
В треугольнике ABC проведена биссектриса AM. Прямая, проходящая через вершину B перпендикулярно AM, пересекает сторону AC в точке N; AB = 6, BC = 5, AC = 9.
а) Докажите, что биссектриса угла C делит отрезок MN пополам.
б) Пусть P - точка пересечения биссектрис треугольника ABC. Найдите отношение AP:PN.
а) Докажите, что биссектриса угла C делит отрезок MN пополам.
б) Пусть P - точка пересечения биссектрис треугольника ABC. Найдите отношение AP:PN.
811.
\[\begin{array}{l}
{\text{На сторонах }}AB,{\text{ }}BC,{\text{ }}CD{\text{ и }}AD{\text{ параллелограмма }}ABCD{\text{ отмечены точки}} \hfill \\
K,{\text{ }}L,{\text{ }}M{\text{ и }}N{\text{ соответственно}}{\text{, причём }}\frac{{AK}}{{KB}} = \frac{{BL}}{{LC}} = \frac{{CM}}{{MD}} = \frac{{DN}}{{NA}}. \hfill \\
{\text{а) Докажите}}{\text{, что четырёхугольник }}KLMN{\text{ - параллелограмм}}{\text{, а его центр}} \hfill \\
{\text{совпадает с центром параллелограмма }}ABCD. \hfill \\
{\text{б) Найдите отношение площадей параллелограммов }}KLMN{\text{ и }}ABCD{\text{, если}} \hfill \\
{\text{известно}}{\text{, что }}AK:KB = 2. \hfill \\
\end{array} \]
929.
\[\begin{array}{l}
{\text{Окружность проходит через вершины }}A,{\text{ }}B{\text{ и }}D{\text{ параллелограмма }}ABCD{\text{,}} \hfill \\
{\text{пересекает сторону }}BC{\text{ в точках }}B{\text{ и }}E{\text{ и пересекает продолжение стороны}} \hfill \\
CD{\text{ за точку }}D{\text{ в точке }}K. \hfill \\
{\text{а) Докажите}}{\text{, что }}AE = AK. \hfill \\
{\text{б) Найдите отношение }}KE:BD{\text{, если }}\angle BAD = {60^ \circ }. \hfill \\
\end{array}\]
1095.
Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.
541.
$$\eqalign{
{\text{В трапеции }}ABCD{\text{ боковая сторона }}AB{\text{ перпендикулярна основаниям}}{\text{.}} \hfill \\
{\text{Из точки }}A{\text{ на сторону }}CD{\text{ опустили перпендикуляр }}AH.{\text{ На стороне}} \hfill \\
AB{\text{ отмечена точка }}E{\text{ так}}{\text{, что прямые }}CD{\text{ и }}CE{\text{ перпендикулярны}}{\text{.}} \hfill \\
{\text{а) Докажите}}{\text{, что прямые }}BH{\text{ и }}ED{\text{ параллельны}}{\text{.}} \hfill \\
{\text{б) Найдите отношение }}BH{\text{ к }}ED{\text{, если }}\angle BCD = {120^ \circ }. \hfill \\
} $$
1093.
\[\begin{array}{l}
{\text{Четырёхугольник }}ABCD{\text{ вписан в окружность радиуса }}R = 8.{\text{ Известно}}{\text{, что}} \hfill \\
AB = BC = CD = 12. \hfill \\
{\text{а) Докажите}}{\text{, что прямые }}BC{\text{ и }}AD{\text{ параллельны}}{\text{.}} \hfill \\
{\text{б) Найдите }}AD. \hfill \\
\end{array}\]
1097.
В остроугольном треугольнике ABC проведены высоты AK и CM. На них из точек M и K опущены перпендикуляры ME и KH соответственно.
а) Докажите, что прямые EH и AC параллельны.
б) Найдите отношение EH к AC, если \[\angle ABC = {30^ \circ }\].
а) Докажите, что прямые EH и AC параллельны.
б) Найдите отношение EH к AC, если \[\angle ABC = {30^ \circ }\].
1101.
В выпуклом четырёхугольнике ABCD точки K, L, M и N - середины сторон AB, BC, CD и AD соответственно. Площади четырёхугольников ABLN и NLCD равны, а площади четырёхугольников KBCM и AKMD относятся как 11:17.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите отношение BC к AD.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите отношение BC к AD.
1104.
Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен \[{\sqrt {23} }\].
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен \[{\sqrt {23} }\].
1107.
Высоты \[B{B_1}\] и \[C{C_1}\] остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что \[\angle B{B_1}{C_1} = \angle BAH\].
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если \[{B_1}{C_1} = 10\sqrt 3 \] и \[\angle BAC = {60^ \circ }\].
а) Докажите, что \[\angle B{B_1}{C_1} = \angle BAH\].
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если \[{B_1}{C_1} = 10\sqrt 3 \] и \[\angle BAC = {60^ \circ }\].
1103.
В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая - боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что \[\frac{{AP}}{{PD}} = \sin D\].
б) Найдите площадь трапеции, если радиусы окружностей равны \[\frac{4}{3}\] и \[\frac{1}{3}\].
а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что \[\frac{{AP}}{{PD}} = \sin D\].
б) Найдите площадь трапеции, если радиусы окружностей равны \[\frac{4}{3}\] и \[\frac{1}{3}\].
1106.
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 4 и MK = 12.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 4 и MK = 12.
1370.
\[\begin{array}{l}
{\text{На стороне }}BA{\text{ угла }}ABC{\text{, равного 3}}{{\text{0}}^ \circ },{\text{ взята такая точка }}D{\text{, что }}AD = 2{\text{ и}} \hfill \\
BD = 1.{\text{ Найдите радиус окружности}}{\text{, проходящей через точки }}A,D{\text{ и}} \hfill \\
{\text{касающейся прямой }}BC. \hfill \\
\end{array}\]
812.
В прямоугольной трапеции меньшее основание равно высоте, а большее основание равно \[a\]. Найдите боковые стороны трапеции, если известно, что одна из них касается окружности, проходящей через концы меньшего основания и касающейся большего основания.
1378.
\[\begin{array}{l}
{\text{Дана трапеция }}ABCD{\text{ с основаниями }}BC{\text{ и }}AD.{\text{ Точки }}M{\text{ и }}N{\text{ являются серединами}} \hfill \\
{\text{сторон }}AB{\text{ и }}CD{\text{ соответственно}}{\text{. Окружность}}{\text{, проходящая через точки }}B{\text{ и }}C{\text{,}} \hfill \\
{\text{пересекает отрезки }}BM{\text{ и }}CN{\text{ в точках }}P{\text{ и }}Q{\text{ (отличных от концов отрезков)}}{\text{.}} \hfill \\
{\text{а) Докажитие}}{\text{, что точки }}M,{\text{ }}N,{\text{ }}P{\text{ и }}Q{\text{ лежат на одной окружности}}{\text{.}} \hfill \\
{\text{б) Найдите }}QN{\text{, если отрезки }}DP{\text{ и }}PC{\text{ перпендикулярны}}{\text{,}} \hfill \\
AB = 21,{\text{ }}BC = 4,{\text{ }}CD = 20,{\text{ }}AD = 17. \hfill \\
\end{array}\]
163.
В равнобедренной трапеции ABCD основание AD в два раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.
б) Пусть O - точка пересечения диагоналей трапеции ABCD. Найдите расстояние от вершины C до середины отрезка OD, если BC = 16 и AB = 10.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.
б) Пусть O - точка пересечения диагоналей трапеции ABCD. Найдите расстояние от вершины C до середины отрезка OD, если BC = 16 и AB = 10.
565.
В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM прямые.
а) Докажите, что BM = CM.
б) Найдите угол ABC, если угол BCD равен \[{64^ \circ }\], а расстояние от точки M до прямой BC равно стороне AD.
а) Докажите, что BM = CM.
б) Найдите угол ABC, если угол BCD равен \[{64^ \circ }\], а расстояние от точки M до прямой BC равно стороне AD.
434.
Сумма оснований трапеции равна 13, диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции взаимно перпендикулярны.
б) Найдите высоту трапеции.
а) Докажите, что диагонали трапеции взаимно перпендикулярны.
б) Найдите высоту трапеции.
888.
\[\begin{array}{l}
{\text{Боковые стороны }}KL{\text{ и }}MN{\text{ трапеции }}KLMN{\text{ равны 8 и 17 соответственно}}{\text{.}} \hfill \\
{\text{Отрезок}}{\text{, соединяющий середины диагоналей}}{\text{, равен 7}}{\text{,5}}{\text{, средняя линия}} \hfill \\
{\text{трапеции равна 17}}{\text{,5}}{\text{. Прямые }}KL{\text{ и }}MN{\text{ пересекаются в точке }}A.{\text{ Найдите}} \hfill \\
{\text{радиус окружности}}{\text{, вписанной в треугольник }}ALM. \hfill \\
\end{array}\]
1089.
\[\begin{array}{l}
{\text{Окружность с центром }}{O_1}{\text{ касается оснований }}BC{\text{ и }}AD{\text{ и боковой стороны }}AB{\text{ трапеции}} \hfill \\
ABCD.{\text{ Окружность с центром }}{O_2}{\text{ касается сторон }}BC,{\text{ }}CD{\text{ и }}AD.{\text{ Известно}}{\text{, что }}AB = 10, \hfill \\
BC = 9,{\text{ }}CD = 30,{\text{ }}AD = 39. \hfill \\
{\text{а) Докажите}}{\text{, что прямая }}{O_1}{O_2}{\text{ параллельна основаниям трапеции }}ABCD. \hfill \\
{\text{б) Найдите }}{O_1}{O_2}. \hfill \\
\end{array}\]
1092.
\[\begin{array}{l}
{\text{Окружность с центром в точке }}O{\text{ высекает на всех сторонах трапеции }}ABCD{\text{ равные хорды}}{\text{.}} \hfill \\
{\text{а) Докажите}}{\text{, что биссектрисы всех углов трапеции пересекаются в одной точке}}{\text{.}} \hfill \\
{\text{б) Найдите высоту трапеции}}{\text{, если окружность пересекает боковую сторону }}AB \hfill \\
{\text{в точках }}K{\text{ и }}L{\text{ так}}{\text{, что }}AK = 15,{\text{ }}KL = 6,{\text{ }}LB = 5. \hfill \\
\end{array}\]
1115.
Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC - биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 12 и BD = 6,5.
а) Докажите, что луч AC - биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 12 и BD = 6,5.
1094.
В трапеции ABCD точка E - середина основания AD, точка M - середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.
а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
6.
\[\begin{array}{l}
{\text{Окружность с центром }}O{\text{, вписанная в треугольник }}ABC{\text{, касается его сторон}}\\
AB,AC{\text{ и }}BC{\text{ в точках }}{C_1},{B_1}{\text{ и }}{A_1}{\text{ соответственно}}{\text{. Биссектриса угла }}A{\text{ пересекает}}\\
{\text{эту окружность в точке }}Q{\text{, лежащей внутри треугольника }}A{B_1}{C_1}.\\
{\text{а) Докажите}}{\text{, что }}{C_1}Q{\text{ - биссектриса угла }}A{C_1}{B_1}.\\
{\text{б) Найдите расстояние от точки }}O{\text{ до центра окружности}}{\text{, вписанной в}}\\
{\text{треугольник }}A{B_1}{C_1}{\text{, если известно}}{\text{, что }}BC = 10,AB = 17,AC = 21.
\end{array}\]
1211.
\[\begin{array}{l}
{\text{Точка }}P{\text{ - центр вписанной окружности треугольника }}ABC.{\text{ Прямые }}AP{\text{ и}} \hfill \\
BP{\text{ пересекают описанную окружность треугольника }}ABC{\text{ в точках }}{A_1}{\text{ и }}{B_1}. \hfill \\
{\text{а) Докажите}}{\text{, что прямая }}CP{\text{ перпендикулярна прямой }}{A_1}{B_1}. \hfill \\
{\text{б) Найдите длину отрезка }}{A_1}{B_1}{\text{, если }}AB = 6,{\text{ }}\angle ACB = {30^ \circ }. \hfill \\
\end{array}\]
1391.
\[\begin{array}{l}
{\text{В треугольнике }}ABC{\text{ }}AB = 11,{\text{ }}BC = 8,{\text{ }}CA = 7.{\text{ Точка }}D{\text{ лежит на прямой }}BC{\text{ так}}{\text{,}} \hfill \\
{\text{что }}BD:DC = 1:6.{\text{ Окружности}}{\text{, вписанные в каждый из треугольников }}ADC{\text{ и}} \hfill \\
ADB{\text{, касаются стороны }}AD{\text{ в точках }}E{\text{ и }}F.{\text{ Найдите длину отрезка }}EF. \hfill \\
\end{array}\]
388.
\[\begin{array}{l}{\text{Точка }}O{\text{ - центр окружности}}{\text{, описанной около остроугольного треугольника}}\\ABC,{\text{ }}I{\text{ - центр вписанной в него окружности}}{\text{, }}H{\text{ - точка пересечения высот}}{\text{.}}\\{\text{Известно}}{\text{, что }}\angle BAC = \angle OBC + \angle OCB.\\{\text{а) Докажите}}{\text{, что точка }}H{\text{ лежит на окружности}}{\text{, описанной около}}\\{\text{треугольника }}BOC.\\{\text{б) Найдите угол }}OHI,{\text{ если }}\angle ABC = {40^ \circ }.\end{array}\]
927.
\[\begin{array}{l}
{\text{Около остроугольного треугольника }}ABC{\text{ с различными сторонами описали}} \hfill \\
{\text{окружность с диаметром }}BN.{\text{ Высота }}BH{\text{ пересекает эту окружность в точке }}K. \hfill \\
{\text{а) Докажите}}{\text{, что }}AN = CK. \hfill \\
{\text{б) Найдите }}KN{\text{, если }}\angle BAC = {35^ \circ },{\text{ }}\angle ACB = {65^ \circ }{\text{, а радиус окружности равен 12}}{\text{.}} \hfill \\
\end{array}\]
1100.
Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L - точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L - точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
1105.
Около остроугольного треугольника ABC описана окружность с центром O. На продолжении отрезка AO за точку O отмечена точка K так, что \[\angle BAC + \angle AKC = {90^ \circ }\].
а) Докажите, что четырёхугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если \[\cos \angle BAC = \frac{3}{5}\], а BC = 48.
а) Докажите, что четырёхугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если \[\cos \angle BAC = \frac{3}{5}\], а BC = 48.
1127.
Две окружности касаются внешним образом в точке C. Прямая касается меньшей окружности в точке A, а большей - в точке B, отличной от A. Прямая AC вторично пересекает бо'льшую окружность в точке D, прямая BC вторично пересекает меньшую окружность в точке E.
а) Докажите, что прямая AE параллельна прямой BD.
б) Пусть L - отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 5.
а) Докажите, что прямая AE параллельна прямой BD.
б) Пусть L - отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 5.
596.
$$\eqalign{
\begin{array}{l}
{\text{В треугольнике }}ABC{\text{ точки }}{A_1},{\text{ }}{B_1}{\text{ и }}{C_1}{\text{ - середины сторон }}BC,{\text{ }}AC{\text{ и }}AB{\text{ соответственно}}{\text{,}}\\
AH{\text{ - высота}}{\text{, }}\angle BAC = {120^ \circ },{\text{ }}\angle BCA = {15^ \circ }.\\
{\text{а) Докажите}}{\text{, что точки }}{A_1},{B_1},{C_1}{\text{ и }}H{\text{ лежат на одной окружности}}{\text{.}}\\
{\text{б) Найдите }}{A_1}H{\text{, если }}BC = 4\sqrt 3 .
\end{array}
} $$
1118.
Высоты тупоугольного треугольника ABC с тупым углом ABC пересекаются в точке H. Угол AHC равен \[{60^ \circ }\].
а) Докажите, что угол ABC равен \[{120^ \circ }\].
б) Найдите BH, если AB = 6, BC = 10.
а) Докажите, что угол ABC равен \[{120^ \circ }\].
б) Найдите BH, если AB = 6, BC = 10.
772.
В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите \[\sin \angle BMC\], если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите \[\sin \angle BMC\], если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
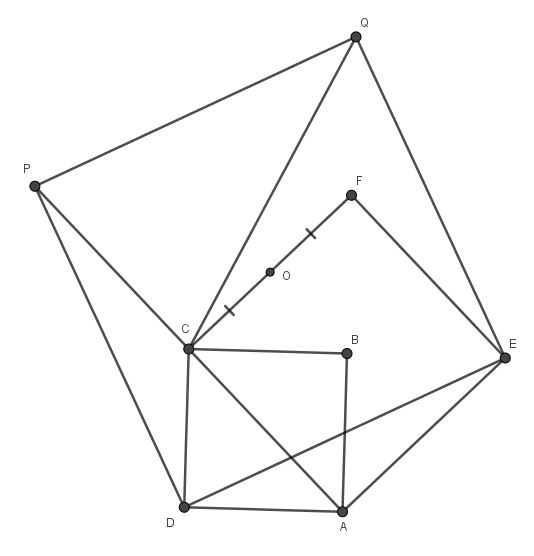
864.
\[\begin{array}{l}
ABCD,{\text{ }}ACFE{\text{ и }}EDPQ{\text{ - квадраты (см}}{\text{. рис}}{\text{.)}}{\text{.}} \hfill \\
CO = OF \hfill \\
{\text{а) Докажите}}{\text{, что }}O{\text{ - центр квадрата }}EDPQ. \hfill \\
{\text{б) Найдите длину отрезка }}CQ{\text{, если }}AB = 1. \hfill \\
\end{array}\]

1121.
Из точки A к окружности проведены касательная AM (M - точка касания) и секущая, пересекающая окружность в точках K и L (AK = AL + LK), такая, что треугольник AMK остроугольный. Расстояние от центра окружности до хорды KM равно половине радиуса окружности.
а) Докажите, что угол AMK равен \[{60^ \circ }\].
б) Найдите площадь треугольника AMK, если L - середина AK и радиус окружности равен 2.
а) Докажите, что угол AMK равен \[{60^ \circ }\].
б) Найдите площадь треугольника AMK, если L - середина AK и радиус окружности равен 2.
